Gaussian Mixture Model (GMM) & Expectation Maximization (EM)

Guassian Model

Gaussian Single Model

Guassian probability model is widely used in machine learning. The density function of single Guassian is: \[ f(x) = \frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(x-\mu)^2}{2\sigma^2}) \]

$$ is the mean and \(\sigma\) is the variance.

\(X\sim N(\mu, \sigma^2)\) means X is distributed according to N.

Multivariate Guassian Model

If \(X = (x_1, x_2, x_3, \dots, x_n)\), the density function is: \[ f(X) = \frac{1}{(2\pi)^{d/2}|\sum|^{1/2}}exp[-\frac 12(X-\mu)^T(\sum )^{-1}(X-\mu)] \]

note: \(d\) is the dimension of variable (\(x_1\)); \(\mu\) is a nx1 matrix, means of each variable.

\(\sum\) is the covariance matrix of \(X\), degree to which \(x_i\) vary together.

For a 2-D Guassian model, \(\sum = \left[ \begin{matrix} \delta_{11} & \delta_{12} \\ \delta_{21} & \delta_{22} \end{matrix} \right]\). \(\sum\) determines the shape of distribution.

Guassian Mixture Model (GMM)

Why GMM

• Some cluster may be 'wider' than others
• Clusters may overlap

If we use one Guassian model, it cannot handle tha data set generated by multi Guassian models, so we introduce GMM -- use multi Gussain models and mix them to one with certain weights.

GMM formula

Assume GMM is mixed by \(\pmb K\) Guassian models, the density fucntion of GMM is: \[ p(X) = \sum_ {k = 1}^K p(k)p(X|k) = \sum_ {k = 1}^K \Pi_ k N(X|\mu_k,\Sigma_ k) \] note: $ p(X|k) = N(X|_ k,()_ k )$ is the density function of \(k^{th}\) Gaussian model. \(\Pi_k\) is the weight and \(\sum_ {k = 1}^{K} \Pi_ {k} = 1\).

So basically GMM is the mixture of multi Gaussian models. In theory, with enough number of mixed Guassian models and proper weights, GMM can fit any distribution.

Examples

Picture1: 1-D GMM

Picture2: 2-D GMM

Picture3: 3-D GMM

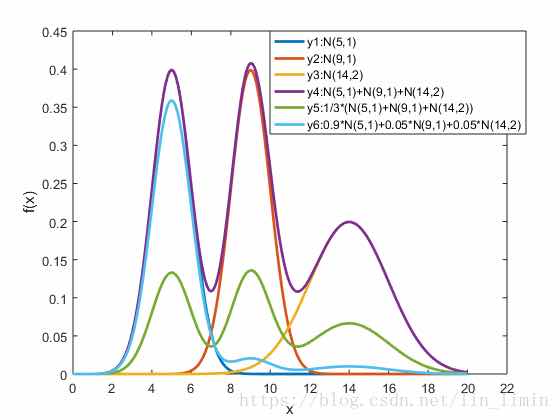
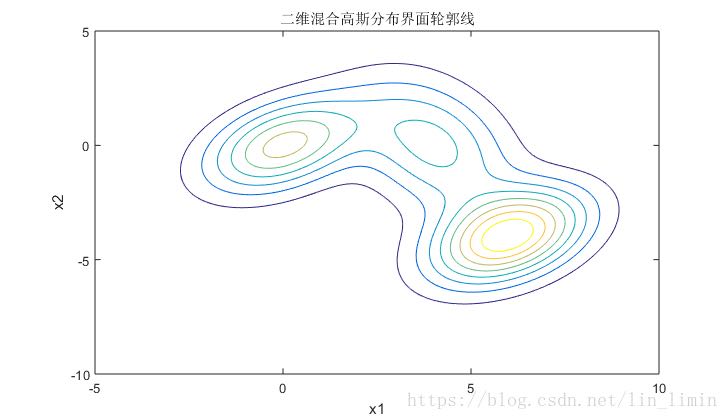
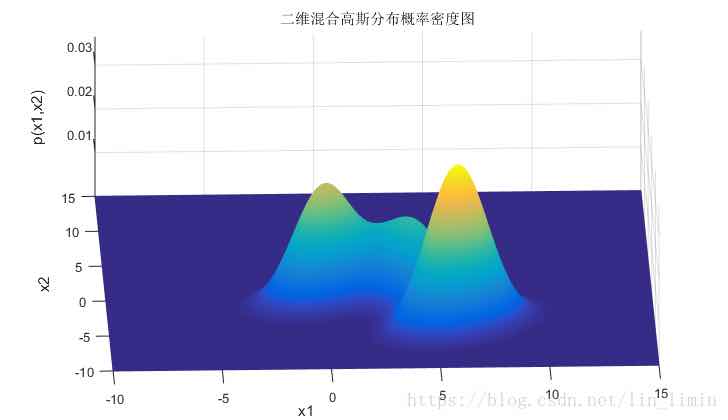
Supervised Learning for GMM

Generating data

1. Choose component (cluster, which Guassian model) \(\pmb i\) with probability \(\pi_ i\).
2. Generate data point from \(N(X|\mu_ i, \Sigma_ i)\).

How to estimate parameters of GMM

• We observe the data points X and their labels y (generate from with Guassian component).

• Maximize the likelihood: \[ \prod_ j P(y_ i = i, X_ j) = \prod_j \pi_ i N(X_ j | \mu_ i, \Sigma_ i) \]

  Product of probability on all the data points ( j ). \(P(y_ i = i)\) means the probabilty of this point is generated by \(i^{th}\) Gaussian component.

• Closed Form Solution

  We have \(m\) data points. For component \(i\), suppose we have \(n\) data points labelled by \(i\). \[ \mu_ i = \frac 1 n \sum_ {j = 1} ^n X_ j \]

  \(\mu_ i\) is the mean of \(i_{th}\) Guassian component, so it should be the mean/center of all data point. \[ \Sigma_ i = \frac 1 n \sum_ {j = 1}^n(X_ j-\mu_ i)(X_ j - \mu_ i)^T \] \((\sum)_ i\) is the covarivance matrix of \(i_ {th}\) Guassian component.

  \(\pi_ i\) is weight, # of points belonging to \(i_ {th}\) Guassian component / # of all points

\[ \pi_ i = \frac nm \]

We have already solved such problem

Unsupervised Learning for GMM

In clusterin, we don't know the labels Y !

• Maximize marginal likelihood: \[ \prod_ j P(X_ j) = \prod_ j\sum_ i P(y_ j = i, X_ j) = \prod_ j\sum_ i \pi_ i N(\mu_ i, \Sigma_ i)P(y_ i = i) \] It is to improve the P of all components

• Parameters to be learnt:

  \(\pi\), \(\mu\), \(\Sigma\), \(y\)

• How to optimize it? (No closed form solution)

  • Expectation Maximization (EM)
    • pick k random Guassian models
    • assign data proportionally to these k models
    • revis model based on the distance between predicted points with real points (just like k-means)

Examples

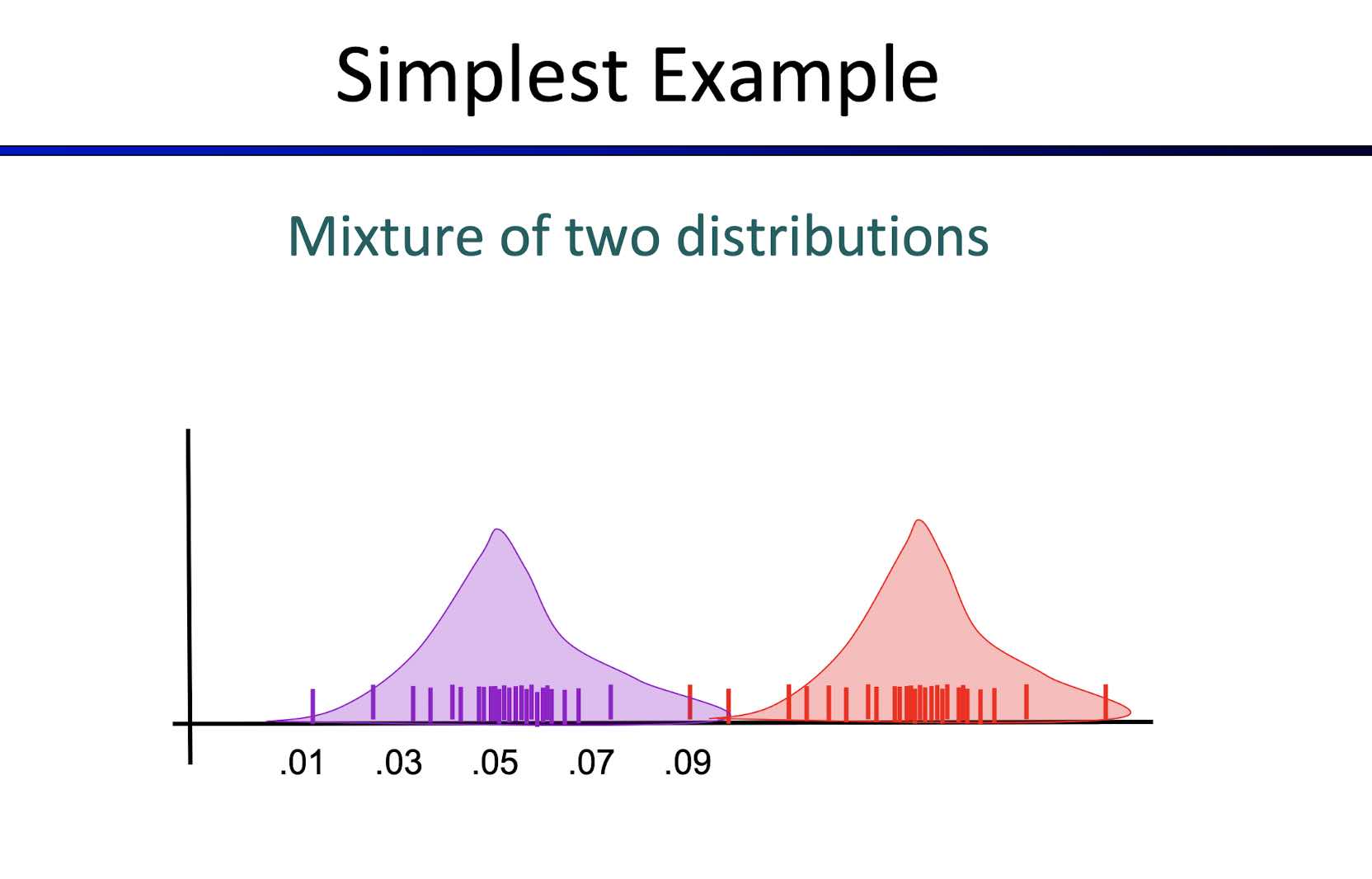
Expectation Maximization (EM)

How it works

Pretend we do know the parameter.

• Initialize randomly
• [E step] Compute probability of each instance having possible label (note: one point shares multiple probabilities corresponding to multiple Guassian models).
• [M step] Treating each instance as fractionally having these labels (one point is treated as having many labels with certain probability), compute the new parameter values.
• Repeat E->M steps

Example

• We get data like this

• Randomly initialize

• Assign labels to point based on current Guassian models

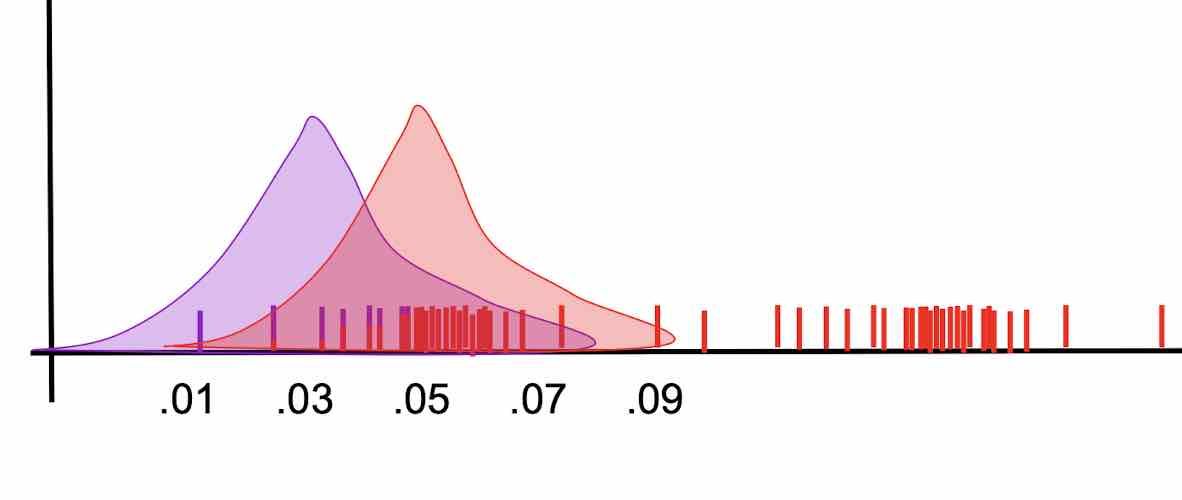
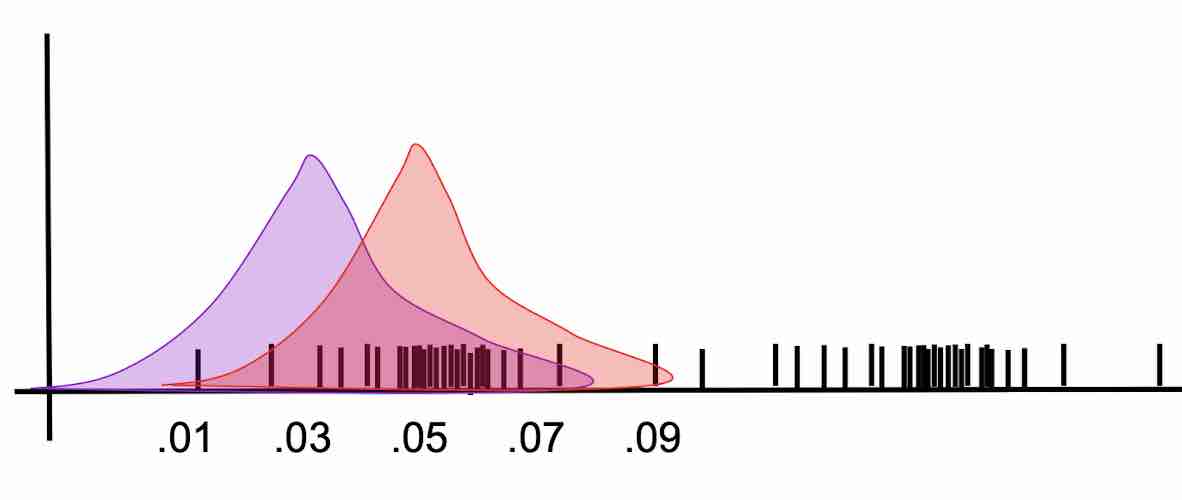
• Recompute the parameters of Guassian models based on current label distribution

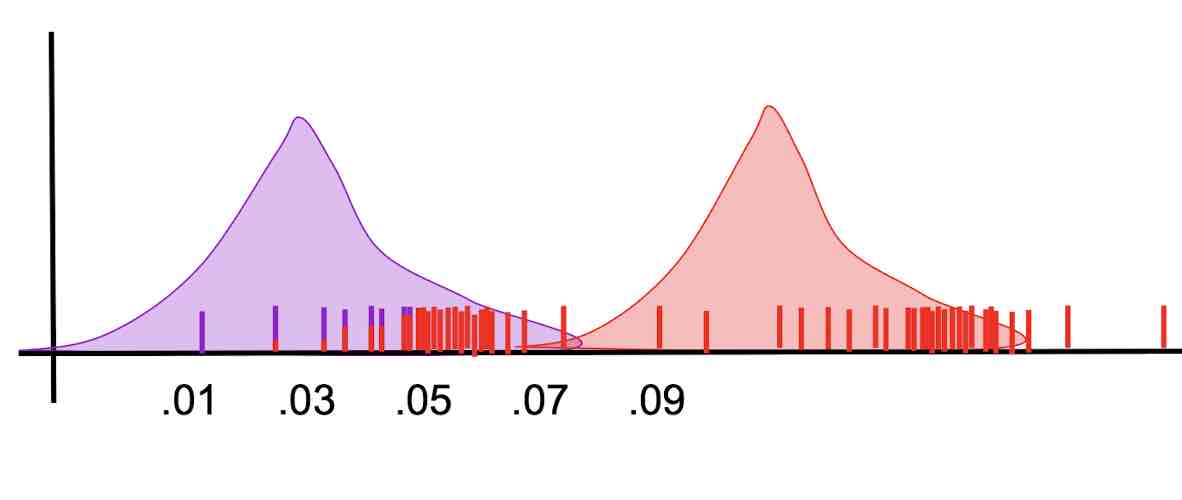
• Repeat--based on current Guassian models, reassign labels to points

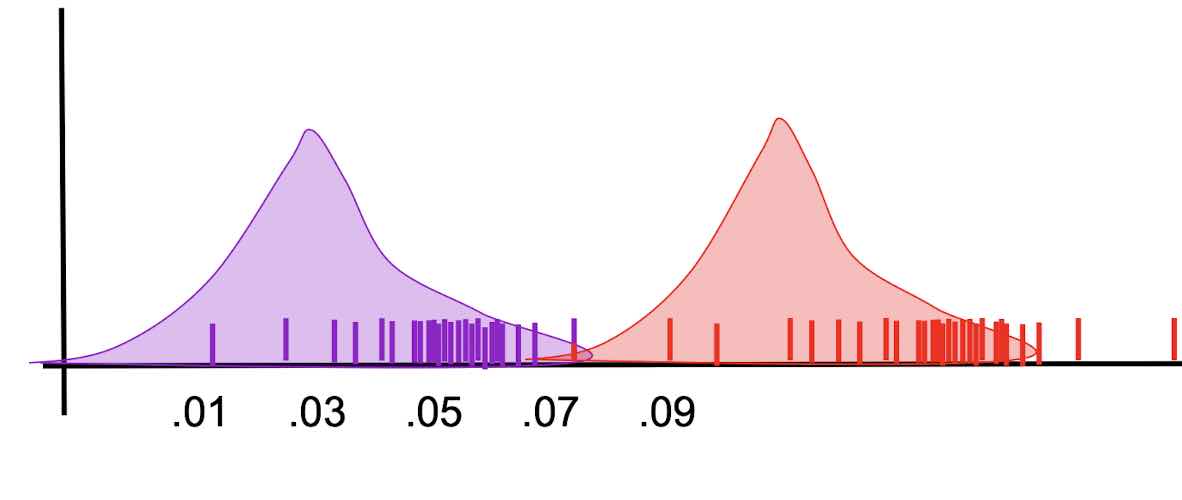
• Stop when no changes

Inclusion

K-means is a special case of GMM--all Gaussians are spherical and have identical weights and covariance (the only parameter is mean).

Extension

In general, EM can be used to learn any model with hidden variables.

EM for HMMs(hidden markov models)--aka. Baum-Welch algorithm

• [M step] compute the distribution of hidden states given each training instance
• [E step] update the parameters to maximize expected log likelihood based on distributions over hidden states.